এই পোস্টে তোমরা পেয়ে যাবে ত্রিভুজ (Triangle) সম্পর্কিত সমস্ত সূত্রাবলি (Formula) ও তথ্য। ত্রিভুজের সংজ্ঞা থেকে শুরু করে বিভিন্ন ত্রিভুজের শ্রেণীবিভাগ, ত্রিভুজের ক্ষেত্রফল, লম্ব, ত্রিভুজের পরিকেন্দ্র, লম্ববিন্দু, ভরকেন্দ্র ইত্যাদি সহ ত্রিভুজের সম্পর্কে সমস্ত কিছু জানতে পারবে এই পোস্টে।
Table of Contents
ত্রিভুজ ও ত্রিভুজ সম্পর্কিত কিছু সূত্র :
ত্রিভুজ কাকে বলে ?
ত্রিভুজের সংজ্ঞা : তিনটি সরলরেখা দ্বারা বেষ্টিত বহুভূজকে ত্রিভুজ বলে। ত্রিভুজের তিনটি শীর্ষবিন্দু (কৌণিক বিন্দু) থাকে।
ইউক্লিডীয়ের সংজ্ঞানুসারে যেকোন তিনটি অসমরেখ বিন্দু একটি অনন্য ত্রিভুজ এবং একই সাথে একটি অনন্য সমতল নির্ধারণ করে। ত্রিভুজই সর্বনিম্ন বহুভুজ।
ত্রিভুজের পরিভাষা সমূহ :
- বাহু বা ভূজ : ত্রিভুজ যে তিনটি সরলরেখা দ্বারা গঠিত তাদের বাহু বা ভূজ বলে। একটি বাহুকে যুক্ত করা বিন্দুর বর্ণ দুটিকে পাশাপাশি লিখে একটি বাহুকে প্রকাশ করা হয়। উদাহরণস্বরূপ চিত্রে AB, BC ও CA হলো ৩টি বাহু। একটি ত্রিভুজের ৩টি বাহুর মধ্যে যেকোনো দুটি বাহুর দৈর্ঘ্যের যোগফল তৃতীয় বাহুর দৈর্ঘ্যের চেয়ে বেশি হতে হবে।
- শীর্ষ বিন্দু : ত্রিভুজের তিনটি বাহু যে তিনটি বিন্দুতে ছেদ করে তাদের শীর্ষ বিন্দু বলে। উপরোক্ত চিত্রে A, B ও C হলো ৩টি শীর্ষবিন্দু।
- ত্রিভুজের পরিসীমা : ত্রিভুজের বাহু তিনটির দৈর্ঘের সমষ্টিকে ত্রিভুজের পরিসীমা বলে।
- ত্রিভুজের ক্ষেত্রফল : ত্রিভুজের ৩টি বাহুর মধ্যবর্তী অঞ্চল বা ক্ষেত্রকে ত্রিভুজের ক্ষেত্রফল বলে। যেকোনো ত্রিভুজের ক্ষেত্রফলের সূত্র = (ভূমির দৈর্ঘ x উচ্চতা) ÷ 2 । এখানের ত্রিভুজের উচ্চতা বলতে ত্রিভুজের যেকোনো শীর্ষবিন্দু থেকে অপর বাহুর উপর অঙ্কিত লম্বকে বোঝায়। আর ভূমি বলতে বোঝায় যে বাহুর ওপর লম্ব টানা হলো সেই বাহুর দৈর্ঘকে।
- ত্রিভুজের কোণ : ত্রিভুজের শীর্ষবিন্দুতে দুটি বাহু যে কোণ সৃষ্টি করে তাকে ত্রিভুজের কোণ বলে। চিত্রে <ABC হলো AB ও BC বাহুর মধ্যবর্তী কোণ। একটি ত্রিভুজের তিনটি শীর্ষকোণের যোগফল ১৮০°।
- পরিকেন্দ্র : ত্রিভুজের বাহুগুলির লম্ব-সমদ্বিখণ্ডক তিনটি যে বিন্দুতে মিলিত হয় তাকে ত্রিভুজের পরিকেন্দ্র বলে।
- মধ্যমা : ত্রিভুজের একটি শীর্ষবিন্দু ও তার বিপরীত বাহুর মধ্যবিন্দুর সংযোগকারী সরলরেখাকে ত্রিভুজের মধ্যমা বলে।
- ভরকেন্দ্র : ত্রিভুজের মধ্যমা তিনটি যে বিন্দুতে মিলিত হয় তাকে ত্রিভুজের ভরকেন্দ্র বলে। যেমন বৃত্ত এবং গোলকের সমস্ত ভর তার কেন্দ্রে থাকে, তেমন ত্রিভুজের সমস্ত ভর তার ভরকেন্দ্র থাকে।
- লম্ববিন্দু : ত্রিভুজের শীর্ষবিন্দুগুলি থেকে বিপরীত বাহুর ওপর অঙ্কিত লম্ব তিনটি যে বিন্দুতে ছেদ করে তাকে ত্রিভুজের লম্ববিন্দু বলে।
ত্রিভুজের প্রকারভেদ :
ত্রিভুজকে বাহুর দৈর্ঘ এবং কোণের ভিত্তিতে ভাগ করা যায়।
বাহুর দৈর্ঘের ভিত্তিতে ত্রিভুজের শ্রেণীবিভাগ :
বাহুর দৈর্ঘের ভিত্তিতে ত্রিভুজকে তিন ভাগে ভাগ করা যায়, যথা :
১) সমবাহু ত্রিভুজ
২) সমদ্বিবাহু ত্রিভুজ
৩) বিষমবাহু ত্রিভুজ
১) সমবাহু ত্রিভুজ :
সংজ্ঞা : যে ত্রিভুজের তিনটি বাহুর দীর্ঘই সমান তাকে সমবাহু ত্রিভুজ বলে। সমবাহু ত্রিভুজের তিনটি শীর্ষকোণও সমান হয়।
উপরোক্ত চিত্রটি সমবাহু ত্রিভুজের উদাহরণ। চিত্রে দেখা যাচ্ছে ত্রিভুজটির প্রতিটি বাহুর দৈর্ঘ সমান অর্থাৎ ‘a’ এবং ৩টি শীর্ষ ত্রিভুজ কোণও সমান (৬০°)।
সমবাহু ত্রিভুজের বৈশিষ্ট ও কিছু সূত্র :
- সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ সমান এবং শীর্ষকোণও সমান (৬০°)।
- সমবাহু ত্রিভুজের প্রতিবাহুর দৈর্ঘ ‘a’ হলে ত্রিভুজের ক্ষেত্রফল =
- সমবাহু ত্রিভুজের মধ্যমা ৩টি সমান এবং এর দৈর্ঘ =
- সমবাহু ত্রিভুজের ভরকেন্দ্র, লম্ববিন্দু ও পরিকেন্দ্র তিনটিই এক।
২) সমদ্বিবাহু ত্রিভুজ :
সংজ্ঞা : যে ত্রিভুজের কমপক্ষে দুইটি বহু সমান তাকে সমদ্বিবাহু ত্রিভুজ বলে। সমবাহু ত্রিভুজকেও সমদ্বিবাহু ত্রিভুজ বলা যায়।
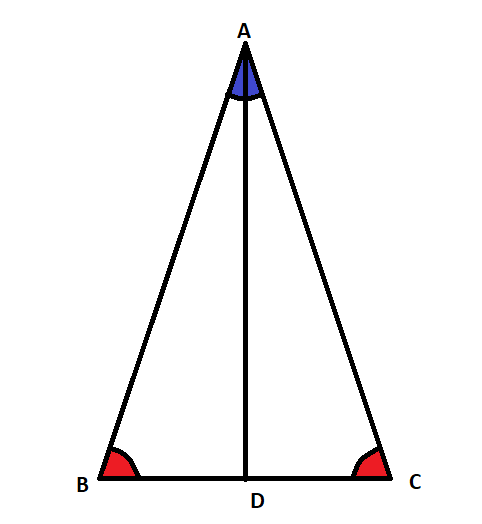
অন্য ভাবে বলতে গেলে যে ত্রিভুজের কমপক্ষে দুটি শীর্ষকোণ সমান তাদের সমদ্বিবাহু ত্রিভুজ বলে। উপরোক্ত চিত্রে দেখা যাচ্ছে ত্রিভুজটির দুটি বাহুর দৈর্ঘ সমান (AB = AC) এবং অসমান বাহুটির দৈর্ঘ BC।
সমদ্বিবাহু ত্রিভুজের বৈশিষ্ট :
- সমদ্বিবাহু ত্রিভুজের কমপক্ষে ২টি বাহুর দৈর্ঘ ও কোণ সমান।
- সমদ্বিবাহু ত্রিভুজের অসমান কোণটির মান
হলে অপর কোণ দুটির মান =
- একটি সমদ্বিবাহু ত্রিভুজের অসমান কোনটির মান ৭০° হলে অপর কোণদুটির মান = ৯০ – (৭০÷২) = ৫৫° ।
- সমদ্বিবাহু ত্রিভুজের অসমান কোণটি থেকে তার বিপরীতে অবস্থিত অসমান বাহুতির ওপর অঙ্কিত লম্ব বা মধ্যমার দৈর্ঘ হলো
৩) বিষমবাহু ত্রিভুজ :
সংজ্ঞা : যে ত্রিভুজের ৩টি বাহুর দৈর্ঘ পরস্পর অসমান তাকে বিষমবাহু ত্রিভুজ বলে।
বিষমবাহু ত্রিভুজের কোনগুলির পরিমাপও অসমান।
বিষমবাহু ত্রিভুজের বৈশিষ্ট :
- বিষমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ ও কোণ অসমান।
- বিষমবাহু ত্রিভুজ সব ত্রিভুজের সাধারণ রূপ।
শীর্ষকোণের ভিত্তিতে ত্রিভুজের শ্রেণীবিভাগ :
শীর্ষকোণের ভিত্তিতে ত্রিভুজকে তিন ভাগে ভাগ করা যায়, যথা :
১) সমকোণী ত্রিভুজ
২) সূক্ষকোণী ত্রিভুজ
৩) স্থূলকোণী ত্রিভুজ
সমকোণী ত্রিভুজ :
সংজ্ঞা : যে ত্রিভুজের একটি কোণের মান ৯০° তাকে সমকোণী ত্রিভুজ বলে। একটি ত্রিভুজের ৩টি কোণের সমষ্টি ১৮০°, তাই একটি ত্রিভুজের একটি কোন ৯০° হলে অপর কোন দুটির যোগফলও ৯০°, অর্থাৎ অপরদুটি কোণই সূক্ষকোণী হবে।
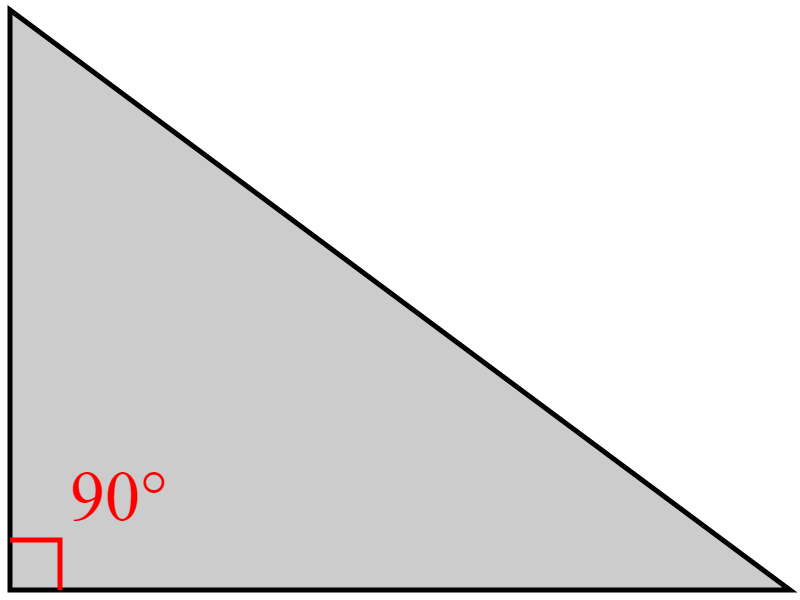
চিত্রে প্রদর্শিত ত্রিভুজটি একটি সমকোণী ত্রিভুজ। একটি সমকোণী ত্রিভুজের দুটি বাহুর দৈর্ঘ সমান হলে বাহুদুটির বিপরীত কোণ দুটির মান = ৯০°÷২ = ৪৫° । এবং এই ত্রিভুজকে সমকোণী-সমদ্বিবাহু ত্রিভুজ বলে।
সমকোণী ত্রিভুজের বৈশিষ্ট :
- সমকোণী ত্রিভুজের একটি কোণের মান ৯০° এবং এই কোণকে সমকোণ বলে।
- সমকোণী ত্রিভুজের সবচেয়ে বড় কোণ, অর্থাৎ সমকোণের (৯০°) বিপরীত বাহুটি ত্রিভুজটির সবচেয়ে বড় বহু এবং এই বাহুটিকে ‘অতিভূজ’ বলা হয়। অপর দুটি বাহুর যেকোনো একটিকে ভূমি ও অপরটিকে লম্ব বলা হয়।
- সমকোণী ত্রিভুজের ভূমির দৈর্ঘ = a; লম্বের দৈর্ঘ্য = b; ও অতিভূজের দৈর্ঘ্য = c হলে পিথাগোরাসের সূত্র ⇒
- সমকোণী ত্রিভুজের ক্ষেত্রফল =
x ভূমি x লম্ব
- সমকোণী ত্রিভুজের একটি সমকোণ
- সমকোণী ত্রিভুজের পরিকেন্দ্র তার অতিভূজের অপর অবস্থান করে।
সূক্ষকোণী ত্রিভুজ :
সংজ্ঞা : যে ত্রিভুজের প্রতিটি কোন সূক্ষকোণ, অর্থাৎ ৯০° এর কম তাকে সূক্ষকোণী ত্রিভুজ বলে।
সমবাহু ত্রিভুজ ও সূক্ষকোণী ত্রিভুজের অন্তর্গত।
সূক্ষকোণী ত্রিভুজের বৈশিষ্ট :
- এই ত্রিভুজের প্রতিটি কোণ সূক্ষকোণ, অর্থাৎ ৯০° এর কম।
- এই ত্রিভুজের পরিকেন্দ্র ত্রিভুজের মধ্যেই থাকে।
স্থূলকোনী ত্রিভুজ :
সংজ্ঞা : যে ত্রিভুজের একটি কোণ স্থূলকোণ, অর্থাৎ ৯০° এর বেশি তাকে স্থূলকোনী ত্রিভুজ বলে।
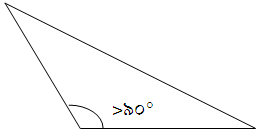
এছাড়া স্থূলকোনী ত্রিভুজের অপর দুটি কোন সূক্ষকোণই হয়।
স্থূলকোনী ত্রিভুজের বৈশিষ্ট :
- স্থূলকোনী ত্রিভুজের একটি শীর্ষকোণ ৯০° এর বেশি হয়।
- স্থূলকোনী ত্রিভুজের পরিকেন্দ্র ত্রিভুজের বাইরে থাকে।
- স্থূলকোনী ত্রিভুজের সূক্ষকোণ দুটির সমষ্টি ৯০° এর কম হয়।
ত্রিভুজ সম্পর্কিত কতগুলি প্রশ্ন ও উত্তর –
ত্রিভুজের তিন কোণের সমষ্টি কত ?
ত্রিভুজের তিন কোণের সমষ্টি ১৮০ ডিগ্রি বা দুই সমকোণ।
ত্রিভুজের মধ্যমা কাকে বলে ?
কোন ত্রিভুজের মধ্যমা হলো সেই রেখাংশ যা ত্রিভুজটির একটি শীর্ষবিন্দুকে শীর্ষবিন্দুটির বিপরীত বাহুর মধ্যবিন্দুর সাথে যুক্ত করে তথা সেই বাহুটিকে সমদ্বিখণ্ডিত করে। সোজা কথায়, ত্রিভুজের শীর্ষবিন্দু এবং এর বিপরীত বাহুর মধ্যবিন্দুর সংযোজক রেখাংশই মধ্যমা।
যে ত্রিভুজের তিনটি কোণই সমান সেই ত্রিভুজ কোন ধরণের ত্রিভুজ ?
যে ত্রিভুজের প্রতিটি কোন সমান সেটি ত্রিভুজের বহু তিনটিও সমান হয়। তাই এই ত্রিভুজকে সমবাহু ত্রিভুজ বলা হয়। আবার এই ত্রিভুজের প্রতিটি কোণ ৬০ ডিগ্রি হবার কারণে এই ধরণের ত্রিভুজ একটি সূক্ষকোণী ত্রিভুজ ।
ত্রিভুজের মোট কয়টি বহু থাকে ?
ত্রিভুজের বহুসংখ্যা ৩টি ।
To check our latest Posts - Click Here
