অংকের সূত্র- পার্ট ১ । Mathematics Formula Part -1 | PDF

প্রিয় পাঠকেরা, তোমাদের জন্য আমরা আজ নিয়ে এসেছি অংকের কিছু সূত্র (Mathematics Formula ) এর তালিকা । কেমন লাগলো কমেন্টের মাধ্যমে জানিও । ভালো লাগলে আমরা এর পরের পার্ট নিয়ে শীঘ্রই চলে আসবো ।

স্বাভাবিক সংখ্যা : 1,2,3,4, . . . .  ইত্যাদি পূর্ণসংখ্যাগুলোর অর্থাৎ ধনাত্মক (অখন্ড) সংখ্যাগুলোকে স্বাভাবিক সংখ্যা বলা হয়। অন্যভাবে বলা যায়, যেসব পূর্ণসংখ্যা গণনার কাজে বা ক্রম নির্দেশ করার কাজে ব্যবহার করা হয় তাদেরকে স্বাভাবিক সংখ্যা বলা হয়।

জোড় সংখ্যা : যেই সংখ্যা 2 দ্বারা পূর্ণ বিভাজ্য তাকে জোড় সংখ্যা বলে। যেমন – 6,10,1024.

বিজোড় সংখ্যা: যেই সংখ্যা 2 দ্বারা পূর্ণ ভাবে বিভাজিত হয় না,তাদের বিজোড় সংখ্যা বলে। যেমন: 3,5,117

মৌলিক সংখ্যা : যেই সংখ্যা কেবল 1 ও সেই সংখ্যা দ্বারা বিভাজ্য ,তাকে মৌলিক সংখ্যা বলে। যেমন :3,5,7

পূর্নবর্গ সংখ্যা: কোনো সংখ্যাকে সেই সংখ্যা দিয়েই গুণ করলে যেই সংখ্যা পাওয়া যায়,তাকে পূর্নবর্গ সংখ্যা বলে।

কোন সংখ্যা কোন সংখ্যা দিয়ে বিভাজ্য দেখার সহজ পদ্ধতি :

• 2 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোন সংখ্যার শেষ অঙ্ক জোড় সংখ্যা বা 0 হলে,সেটি 2 দ্বারা বিভাজ্য হবে।
• 3 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোন সংখ্যার অঙ্ক গুলির সমষ্টি 3 দ্বারা বিভাজ্য হলে সংখ্যাটি 3 দ্বারা বিভাজ্য হবে।
• 4 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোনো সংখ্যার শেষ দুটি অঙ্ক 4 দিয়ে বিভাজ্য  হলে অথবা শেষদুটি অঙ্ক 00 হলে সংখ্যাটি 4 দ্বারা বিভাজ্য হবে।
• 5 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোন সংখ্যার শেষ অঙ্ক 0 অথবা 5 হলে সংখ্যাটি 5 দ্বারা বিভাজ্য হবে।
• 6 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোন যুগ্ম সংখ্যার অঙ্ক গুলির সমষ্টি 3 দ্বারা বিভাজ্য হলে সংখ্যাটি ৬ দ্বারা বিভাজ্য হবে।
• 7 দ্বারা বিভাজ্য হওয়ার নিয়ম: একটি সংখ্যার একক স্থানীয় অঙ্ক কে 2 দিয়ে গুণ করে বাকি সংখ্যা গুলি থেকে বিয়োগ করলে, বিয়োগফল যদি 7 দ্বারা বিভাজ্য হয় তাহলে সংখ্যাটি 7 দ্বারা বিভাজ্য হবে।
• 8 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোন সংখ্যার শেষ 3 টি অঙ্ক 8 দ্বারা বিভাজ্য হলে অথবা শেষ তিনটি অঙ্ক 0 হলে সংখ্যা টি 8 দ্বারা বিভাজ্য হবে।
• 9 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোন সংখ্যার অঙ্ক গুলির সমষ্টি 9 দ্বারা বিভাজ্য হলে সংখ্যাটি 9 দ্বারা বিভাজ্য হবে।
• 10 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোন সংখ্যার শেষ অঙ্ক 0  হলে সংখ্যাটি 10 দ্বারা বিভাজ্য হবে।
• 11 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোন সংখ্যার যুগ্ম স্থানীয় অঙ্কের সমষ্টি ও অযুগ্ম স্থানের অঙ্কের সমষ্টির, অন্তর 0 অথবা 11 এর গুণিতক হলে,সেই সংখ্যাটি 11 দ্বারা বিভাজ্য হবে।
• 12 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোন সংখ্যা 3 ও 4 উভয় দ্বারা বিভাজ্য হলে সংখ্যাটি 12 দ্বারা বিভাজ্য হবে।
• 13 দ্বারা বিভাজ্য হওয়ার নিয়ম: একটি সংখ্যার একক স্থানীয় অঙ্ক কে 4 দিয়ে গুণ করে বাকি সংখ্যা গুলির সাথে যোগ করলে, যোগফল যদি 13 দ্বারা বিভাজ্য হয় তাহলে সংখ্যাটি 13 দ্বারা বিভাজ্য হবে।
• 14 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোন যুগ্ম সংখ্যা 7 দ্বারা বিভাজ্য হলে সংখ্যাটি 14 দ্বারা বিভাজ্য হবে।
• 15 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোন সংখ্যা 3 ও 5 উভয় দ্বারা বিভাজ্য হলে সংখ্যাটি 15 দ্বারা বিভাজ্য হবে।
• 20 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোন সংখ্যার শেষ অঙ্কটি 0 ও শেষের আগের অঙ্কটি জোড় সংখ্যা হলে, সংখ্যাটি 20 দ্বারা বিভাজ্য হবে।
• 25 দ্বারা বিভাজ্য হওয়ার নিয়ম: কোন সংখ্যার শেষ অঙ্ক দুটি 25/50/75/00 হলে সংখ্যাটি 25 দ্বারা বিভাজ্য হবে।

পাটিগণিতের কিছু গুরুত্বপূর্ণ সূত্র :

1. ল.সা.গু.,গ.সা.গু :
   • দুটি সংখ্যার ল.সা.গু × গ.সা.গু = সংখ্যা দুটির গুণফল।
   • দুটি পরস্পর মৌলিক সংখ্যা/দুটি ক্রমিক সংখ্যার গ.সা.গু =1, ল.সা.গু = সংখ্যা দুটির গুণফল.
   • ভগ্নাংশের গ.সা.ণ্ড = লবণ্ডলোর গ.সা.ণ্ড  ÷ হরণ্ডলোর  ল.সা.ণ্ড
   • ভগ্নাংশের  ল.সা.ণ্ড = লবণ্ডলোর  ল.সা.ণ্ড  ÷ হরণ্ডলোর  গ.সা.ণ্ড
   • গ.সা.ণ্ড = সংখ্যা দুটির ণ্ডনফল ÷ ল.সা.ণ্ড
   • ল.সা.ণ্ড = সংখ্যা দুটির ণ্ডনফল ÷ গ.সা.ণ্ড

2. সমান্তর প্রগতির (Arithmetic Progression)
কোনো সমান্তর প্রগতির প্রথম পদ a, শেষ পদ l, সাধারণ অন্তর =d, পদ সংখ্যা =n , হলে –

• • সমান্তর প্রগতির যোগফল=n/2(a+l) =ⁿ⁄₂ ×[2a+(n-1)×d]
  • সমান্তর প্রগতির গড় =(a+l)÷2
  • সমান্তর প্রগতির পদসংখ্যা= {(a – l)÷ d} + 1
  •  কোন সমান্তর প্রগতির n তম সংখ্যা = a + (n -1) ×d

3. গুন্নতর প্রগতি (Geometric Progression)
কোনো গুন্নতর প্রগতির প্রথম পদ a, সাধারণ অনুপাত r, পদ সংখ্যা n হলে,

• • গুন্নতর প্রগতির n তম পদ =a×r^(n-1)
  • গুন্নতর প্রগতির যোগফল =
    a×(1 – rⁿ)/(1-r),   যখন r ≠1
    অসীম পর্যন্ত যোগফল = ^a⁄_(r-1) , যেখানে, r<1

4. সরল সুদ ( Simple Interest )  :
   যদি মোট সুদ = I ,আসল = P, শতকরা বার্ষিক সুদের হার = R%, সময় = T বছর,  তবে –
   • মোট সুদ = ( আসল × সময় × বার্ষিক সুদের হার ) ÷ 100
     অর্থাৎ, I=PRT/100
   • সবৃদ্ধিমুল ( A ) = আসল + মোট সুদ = P + I = P +  I = P(1+RT/100)
   • বার্ষিক সুদের হার =R= (I*100)÷(P*T)

5. চক্রবৃদ্ধি সুদ ( Compound Interest ):

যদি P = আসল বা মূলধন , r% = বার্ষিক সুদের হার হয়

• n বছরের সুদ=I= P(1+r/100)ⁿ -P
• n বছরের সুদ আসল =A= P(1+r/100)ⁿ
•  A=P(1+r/200)²ⁿ , যখন প্রতি ছয় মাস অন্তর চক্রবৃদ্ধির সুদ হিসাব করা হয়। এক্ষেত্রে 2n = সুদ পর্বসংখ্যা , n = বছরের সংখ্যা।
• A=P(1+r/400)⁴ⁿ , যখন প্রতি তিন মাস অন্তর চক্রবৃদ্ধির সুদ হিসাব করা হয়।এক্ষেত্রে 4n = সুদ পর্বসংখ্যা , n = বছরের সংখ্যা।

বীজগাণিতিক কিছু গুরুত্বপূর্ণ সূত্র:

বর্গ নির্ণয়:

1. (a + b)² = a² + 2ab + b²  =(a – b)² + 4ab
2. (a – b)² = a² – 2ab + b²  =(a + b)² – 4ab
3. (a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
4. a² + b² = (a – b)² + 2ab = (a + b)² – 2ab
5. 4ab = (a + b)² – (a – b)²
6. (a – b)² = (a + b)² – 4ab
7. ab = {(a + b)/2}² – {(a – b)/2}²
8. 2(a² + b²) = (a + b)² + (a – b)²
9. a² + b² + c² =(a + b+ c)² – 2(ab + bc + ca)
10. (a + b + c)² = a² + b² + c² + 2(ab + bc + ca) =a² + b² + c² + 2abc(1/a + 1/b + 1/c)

ঘন নির্ণয়ের সূত্র:-

1. (a + b)³ = a³ + b³ + 3ab (a + b) = a³ + 3a²b + 3ab² + b³
2. (a – b)³= a³ – b³ – 3ab (a – b) = a³ – 3a²b + 3ab² – b³
3. a³ + b³ = (a + b) (a² – ab + b²) =  (a + b)³ – 3ab (a + b)
4. a³ – b³ = (a – b) (a² + ab + b²) = (a – b)³ + 3ab (a – b)
5. a³ + b³ + c³ – 3abc = (a+b+c)(a² + b² + c² -ab -bc -ca)

আরো কিছু সূত্র:

1. a⁴ – b⁴ = (a² + b²)(a² – b²)
2. a⁴ + a² + 1 =(a² + a + 1)(a² – a +1)
3. aⁿ – bⁿ =(a – b){a^(n-1) + a^(n-2)*b +….+b^(n-1)}

পরিমিতির কিছু গুরুত্বপূর্ণ সূত্র

1. কোন ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য a,b ও c একক এবং a ও b এর মধ্যবর্তী কোণ α হলে,
   • পরিসীমা = a + b +c একক
   • অর্ধ পরিসীমা =s = (a + b +c)/2 একক।
   • ক্ষেত্রফল = {s*(s-a)*(s-b)*(s-c)}^½
   • ক্ষেত্রফল = ½a*b*sinα বর্গএকক।
2. সমবাহু ত্রিভুজের একটি বাহুর দৈর্ঘ্য a একক হলে,
   • পরিসীমা = 3a  একক
   • উচ্চতা=√3/2 a একক
   • ক্ষেত্রফল = √3/4 *a² বর্গএকক
3. সমদ্বিবাহুবাহু ত্রিভুজের সমান বাহু দুটির দৈর্ঘ্য a একক হলে এবং অপর বাহুর দৈর্ঘ্য b একক হলে,
   • পরিসীমা = (2a+b) একক
   • ক্ষেত্রফল ={(b/4)*(4a² – b²)}^½ বর্গএকক
4. আয়তক্ষেত্রের পরিসীমা = 2 ×(দৈর্ঘ্য+প্রস্থ) একক
5. আয়তক্ষেত্রের ক্ষেত্রফল = (দৈর্ঘ্য×প্রস্থ) বর্গ একক
6. আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য =(দৈর্ঘ্য ²+প্রস্থ ²)^½
7. বর্গক্ষেত্রের পরিসীমা =4× বাহুর দৈর্ঘ্য। একক
8. বর্গক্ষেত্রের ক্ষেত্রফল = (বাহু)² = ½*(কর্ণের দৈর্ঘ্য) ² বর্গএকক
9. বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য =2×(বাহুর দৈর্ঘ্য)^½ একক
10. সামান্তরিকের পরিসীমা =2×(সন্নিহিত বাহু দুটির দৈর্ঘ্য) একক
11. সামান্তরিকের ক্ষেত্রফল = ভূমি×উচ্চতা (বর্গ একক) বর্গএকক
12. সামান্তরিকের সন্নিহিত বাহু দুটির দৈর্ঘ্য a ও b এবং তাদের মধ্যবর্তী কোণ α হলে, ক্ষেত্রফল= a*b*sin α বর্গএকক
13. সামান্তরিকের একটি কর্ণ d ও বিপরীত শীর্ষবিন্দু থেকে কর্ণের উপর লম্বের দৈর্ঘ্য h হলে,ক্ষেত্রফল = d*h বর্গএকক
14. ট্রাপিজিয়ামের সমান্তরাল বাহুদুটির দৈর্ঘ্য a ও b এবং উচ্চতা h একক হলে,
    • ক্ষেত্রফল = ½*h*(a+b) বর্গএকক
15. রম্বসের একটি বাহুর দৈর্ঘ্য a এবং কর্ণ দুটি d1,d2 হলে,
    • পরিসীমা =4×a একক
    • ক্ষেত্রফল =½*(d1 * d2) বর্গএকক
16. আয়তাকার ঘনবস্তুর দৈর্ঘ্য=a একক প্রস্থ=b একক ,উচ্চতা =h একক হলে
    • কর্ণের দৈর্ঘ্য =(a² + b² + c²)^½
    • সমগ্রতলের ক্ষেত্রফল=2(ab×bc×ca)  বর্গএকক
    • চার দেয়ালের ক্ষেত্রফল = 2(a + b) ×h বর্গএকক
    • আয়তন =a × b × h ঘনএকক
17. কোনো ঘনকের দৈর্ঘ্য=a একক,উচ্চতা =h একক হলে
    • কর্ণের দৈর্ঘ্য =a√3 একক
    • সমগ্রতলের ক্ষেত্রফল=6a² বর্গএকক
    • পৃষ্ঠ তলের কর্ণের দৈর্ঘ্য = a√2
    • আয়তন =a³ ঘনএকক
18. কোনো বৃত্তের ব্যাসার্ধ r একক এবং কেন্দ্রে চাপের কোণ α হলে,
    • ব্যাস=2r একক
    • পরিধি =2πr একক
    • ক্ষেত্রফল = πr² বর্গএকক
19. কোন গোলকের ব্যাসার্ধ r একক হলে,
    • তলের ক্ষেত্রফল =4πr² বর্গএকক
    • গোলকের আয়তন =4/3 *πr³
20. কোন অর্ধগোলকের ব্যাসার্ধ r একক হলে,
    • তলের ক্ষেত্রফল =3πr² বর্গএকক
    • অর্ধগোলকের আয়তন =2/3 πr³
21. সমবৃত্তভূমিক কোণকের/শঙ্কুর ভূমির ব্যাসার্ধ r একক, উচ্চতা h একক,হেলান উন্নতি l একক হলে,
    • l =(r² + h²)^½ একক
    • বক্রতলের ক্ষেত্রফল =πrl বর্গএকক
    • সমগ্রতলের ক্ষেত্রফল =πr(r +l ) বর্গএকক
    • আয়তন =⅓*πr²h ঘনএকক
22. সমবৃত্তভূমিক বেলনের/চোঙের ভূমির ব্যাসার্ধ r একক, উচ্চতা h একক,হেলান উন্নতি l একক হলে,
    • বক্রতলের ক্ষেত্রফল =2πrh বর্গএকক
    • সমগ্রতলের ক্ষেত্রফল =2πr(r+h) বর্গএকক
    •  আয়তন =πr²h ঘনএকক

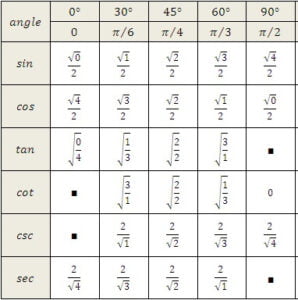
ত্রিকোণমিতির কিছু গুরুত্বপূর্ণ সূত্র :

• sin θ = 1/cosec θ =লম্ব/অতিভুজ
• cos θ = 1/sec θ =ভূমি/অতিভুজ
• tan θ = 1/cot θ =লম্ব/ভূমি
• cosec θ = 1/sin θ =অতিভুজ/লম্ব
• sec θ = 1/cos θ = অতিভুজ/ভূমি
• cot θ = 1/tan θ =ভূমি /লম্ব
• sin(90°−x) = cos x
• cos(90°−x) = sin x
• tan(90°−x) = cot x
• cot(90°−x) = tan x
• sec(90°−x) = cosec x
• cosec(90°−x) = sec x

• sin (3π/2 – A)  = – cos A
• cos (3π/2 – A)  = – sin A
• sin (3π/2 + A) = – cos A
• cos (3π/2 + A) = sin A
• sin (π – A) = sin A
• cos (π – A) = – cos A
• sin (π + A) = – sin A
• cos (π + A) = – cos A
• sin (2π – A) = – sin A
• cos (2π – A) = cos A
• sin (2π + A) = sin A
• cos (2π + A) = cos A

1. sin(A – B) = sinA.cosB – cosA.sinB
2. sin(A + B) = sinA.cosB + cosA.sinB
3. cos(A + B) = cosA.cosB – sinA.sinB
4. cos(A – B) = cosA.cosB + sinA.sinB
5. tan(A + B) = (tanA + tanB)/(1 – tanA.tanB)
6. tan(A – B) = (tanA – tanB)/(1+ tanA.tanB)
7. cot(A – B) = (cotA.cotB + 1)/(cotB – cotA)
8. cot(A + B) = (cotA.cotB – 1)/(cotA + cotB)
9. cos(A + B).cos(A – B) = cos2A – sin2B = cos2B – sin2A
10. sin(A + B).sin(A – B) = sin2A – sin2B = cos2B – cos2A
11. sinx+siny=2sin{(x+y)/2}*cos{(x−y)/2}
12. sinx−siny=2cos{(x+y)/2}*sin{(x-y)/2}
13. cosx+cosy=2cos{(x+y)/2}*cos{(x-y)/2}
14. cosx−cosy=−2sin{(x+y)/2}*sin {(x-y)/2}
15. sin(2x) = 2sin(x) • cos(x) = [2tan x/(1+tan²x)]
16. cos(2x) = cos²x–sin²x = [(1-tan²x)/(1+tan² x)]
17. cos(2x) = 2cos²x −1 = 1–2sin²x
18. tan(2x) = [2tan(x)]/ [1−tan²(x)]
19. sec (2x) = sec2 x/(2-sec2 x)
20. cosec (2x) = (sec x. cosec x)/2
21. Sin 3x = 3sin x – 4sin3x
22. Cos 3x = 4cos3x-3cos x
23. Tan 3x = [3tanx-tan³x]/[1-3tan²x]

Download in PDF Format :


Download

আরো দেখে নাও

Report Writing Step by Step | WBPSC Clerkship | ICDS | WBCS Mains

Precis Writing &#8211; Rules, Dos & Don’ts